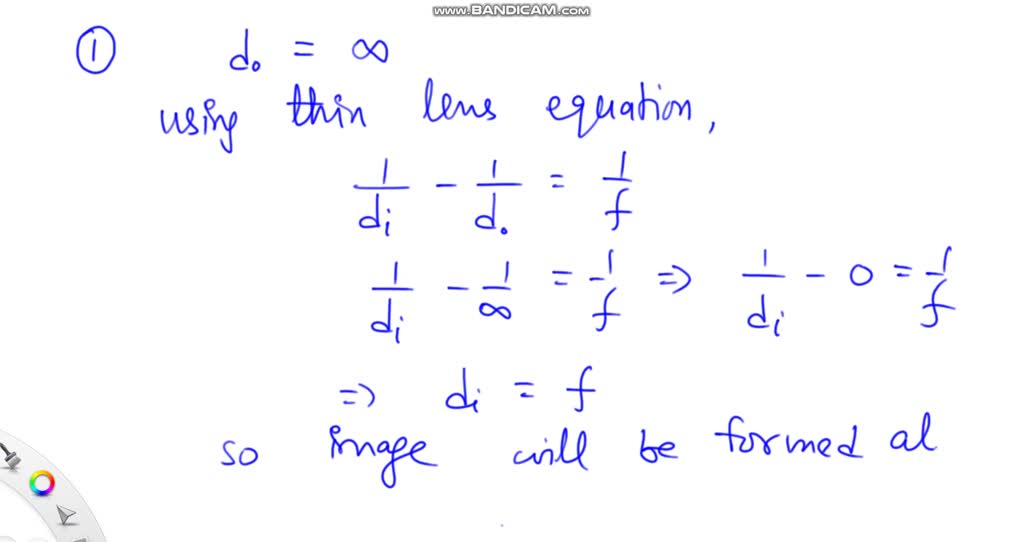Virbhadra–Ellis lens equation

The Virbhadra-Ellis lens equation in astronomy and mathematics relates to the angular positions of an unlensed source ${\displaystyle \left(\beta \right)}$, the image ${\displaystyle \left(\theta \right)}$, the Einstein bending angle of light ${\displaystyle ({\hat {\alpha }})}$, and the angular diameter lens-source ${\displaystyle \left(D_{ds}\right)}$ and observer-source ${\displaystyle \left(D_{s}\right)}$ distances.

${\displaystyle \tan \beta =\tan \theta -{\frac {D_{ds}}{D_{s}}}\left[\tan \theta \tan \left({\hat {\alpha }}-\theta \right)\right]}$.

This approximate lens equation is useful for studying the gravitational lens in strong and weak gravitational fields when the angular source position is small.

References